Our primitive ancestors left many paintings on the walls inside caves. Additionally, inside and near these places there is evidence of fire pits, and refuse and burial sites. However, one could equally imagine this same evidence of daily life on exposed cliffs or hillsides, on trees or animals skins, and beside rivers and coastlines. Such evidence, if it existed, would have long been washed, eroded, or rotted away. Thus, prehistoric people are characterised as ‘cavemen’, presumed to have a predilection for dwelling in these places only because that is where most evidence is taken. This ‘caveman effect’ is an example of what is known as ‘sampling bias’ — one of the biggest problems when conducting any form of statistical data gathering.
Surveys, for example, are popular because they are easy to administer and relatively cost-effective, particularly if conducted remotely through technical means, such as telephone, mail, email, or the Internet. Surveys also lend themselves to obtaining particularly large numbers of respondents, which, in theory, allows a greater chance of sampling all the variations of the target population. They can also be standardised with fixed questions and responses (such as ‘tick the box’ or ‘closed-ended’ questions). This allows easy collation, analysis, and presentation of results, all with the air of precision that mathematics brings. Such surveys, however, have proven notoriously unreliable because of the difficulty in obtaining representative samples. In other words, the sampling is biased, or skewed in favour of certain outcomes.
Let us look at some examples. If one calls people on cellphones, it immediately excludes those who favour landlines, and thus the sample of respondents may be those who are more technically-conversant, skewing data based on, say, technical issues (‘How often do you use the Internet?’). If one rings domestic homes during the daytime, most of those who work during the day will be excluded. Those that answer will more likely be the unemployed, disabled, elderly, and retired, skewing data based on, say, work-related issues (‘How important is work in your life?’). No matter how large the sampling size is, sampling bias can immediately invalidate the results.
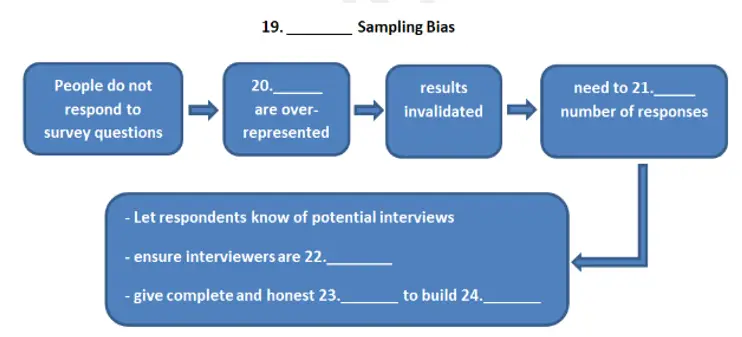
One of the more subtle of sampling biases is known as self-selection. No matter how rigorously the respondents are chosen to be random and characteristic of the target population, those who choose to respond will be different to those who do not. Generally, respondents who are willing to invest time in giving answers obviously want to say something, whereas those who choose not to answer probably do not. Thus, any survey in which many respondents do not answer, do not give clear answers, or only give cursory or unthinking answers, is immediately invalidated, since opinionated perspectives are disproportionately represented.
The latter is such an immediate and obvious problem that it has given rise to techniques to maximise the possibility of garnering responses. One of the more effective is to give the respondents advanced warning (often through the mail), highlighting the time, the nature of the survey, and the mode of delivery, as well as expressing appreciation for the assistance. The interviewers themselves must be sufficiently trained in correct question-asking techniques, and, with cranks, salespeople, and scam-artists abounding, interviewers must provide introductions about themselves, their company, and the nature of the interview, fully and with evident sincerity, in order to gain the trust of those they are talking to.
Even with this, sampling bias can easily arise due to the number of variables in place, since it only takes one to skew the data. If taking samples from a specific location — say, a street corner—then it may be that this location is in the business district, excluding ordinary workers from the sample. It may be that it is near a restaurant district, excluding those who cook more often for themselves. If there is a health club nearby, the majority of respondents may be much healthier than the average of the population. If it is on a university campus, designed to poll university students, is it near the engineering or the arts faculty? The part-time or full-time schools? Are they rich or poor? Male or female? What about race, colour, gender, religion, socio-economic background, and first language? The list goes on and on.
One method to deal with this is to make sure all targeted groups are represented, if only a little, and make mathematical extrapolations to correct the bias. For this to work, the degree of underrepresentation needs to be quantified exactly, and one needs to assume the under-represented respondents are indeed typical of their kind. If, for example, one aims to find the opinion of the population regarding the outcome of an election, but could only, for whatever reasons, interview one woman for every four men, the responses of the women could be multiplied by four, and thus, one can assume (guardedly and with many provisos), that the sampling bias from gender has been corrected. But that does assume all the other variables which introduce bias have been excluded — often a very problematic assumption to make.
Questions 14-18
Do the following statements agree with the information given in Reading Passage Two?
TRUE if the statement agrees with the information
FALSE if the statement contradicts the information
NOT GIVEN If there is no information on this
14. Cavemen were often very good artists.
15. Surveys can be done cheaply by telephone.
16. Surveys can usually give reliable information.
17. The elderly and disabled people are often at home during the day.
18. Larger survey samples can reduce sampling bias.
Questions 19-24
Complete the flowchart. Choose NO MORE THAN TWO WORDS from the passage for each answer.
Questions 25-26
Choose the correct letter, A, B, C, or D.
25. The number of sampling variables
A is usually not so large.
B can result in important input being lost.
C means many locations need to be used.
D can result in lists being necessary.
26. Mathematical extrapolation
A can yield confident results.
B requires responses from both men and women.
C needs exact ratios.
D needs many respondents.
